Checking Collinearity of 3 points and their orientation

Collinear points are those which lies on a single straight line. We have 3 points in the X-Y plane with their (x,y) coordinates given. To find out if the given 3 points are collinear, we will check the angle which the lines between each pair of points make with the X-axis. If the angles are same then the points are collinear.

We have points p1,p2, and p3 given. Lets see the different cases:-

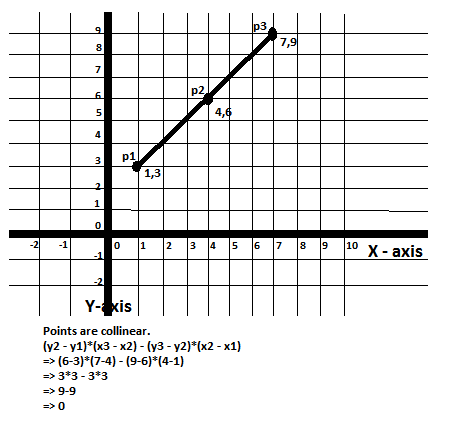
1. Points are collinear

Let us consider the following three points:-
p1  -> (1,3)
p2 -> (4,6)
p3 -> (7,9)

In this case the angle which the line (p1,p2) makes with the X-axis is same as the angle which the line(p2,p3) makes with the X-axis. Hence the points are collinear.

Proof:-

The angle for line (p1,p2) = (y2 – y1)/(x2 – x1)
The angle for line (p2,p3) = (y3 – y2)/(x3 – x2)
As the angles are same, we have :
=> (y2 – y1)/(x2 – x1) = (y3 – y2)/(x3 – x2)
=> (y2 – y1)*(x3 – x2) = (y3 – y2)*(x2 – x1)

Hence we get,
=> (y2 – y1)*(x3 – x2) – (y3 – y2)*(x2 – x1) = 0

So to check the collinearity of 3 points, the following expression should hold true:-
(y2 – y1)*(x3 – x2) – (y3 – y2)*(x2 – x1) = 0

Following figure shows 3 collinear points and the value of the above expression:-

 

2. Points p3 lies clockwise to the line (p1,p2) 

Let us consider the following three points:-
p1  -> (1,3)
p2 -> (4,6)
p3 -> (8,7)

In this case the angle which the line (p1,p2) makes with the X-axis is greater than the angle which the line(p2,p3) makes with the X-axis.

The angle for line (p1,p2) = (y2 – y1)/(x2 – x1)
The angle for line (p2,p3) = (y3 – y2)/(x3 – x2)
As the angle for line (p1,p2) is greater we have :
=> (y2 – y1)/(x2 – x1) > (y3 – y2)/(x3 – x2)
=> (y2 – y1)*(x3 – x2) > (y3 – y2)*(x2 – x1)

Hence we get,
=> (y2 – y1)*(x3 – x2) – (y3 – y2)*(x2 – x1) > 0

So if the value of the above expression is greater than 0, then the point p3 lies to the clockwise of line (p1,p2).

 

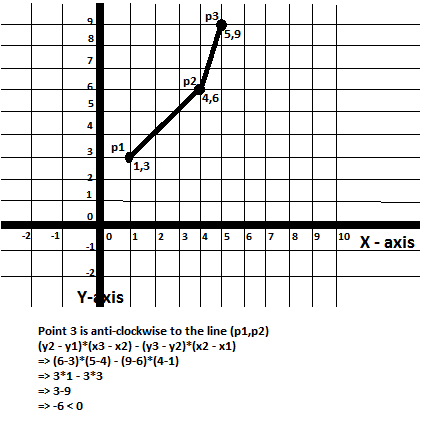
3. Points p3 lies anti-clockwise to the line (p1,p2)

Let us consider the following three points:-
p1  -> (1,3)
p2 -> (4,6)
p3 -> (5,9)

In this case the angle which the line (p1,p2) makes with the X-axis is smaller than the angle which the line(p2,p3) makes with the X-axis.

The angle for line (p1,p2) = (y2 – y1)/(x2 – x1)
The angle for line (p2,p3) = (y3 – y2)/(x3 – x2)
As the angle for line (p1,p2) is greater we have :
=> (y2 – y1)/(x2 – x1) < (y3 – y2)/(x3 – x2)
=> (y2 – y1)*(x3 – x2) < (y3 – y2)*(x2 – x1)

Hence we get,
=> (y2 – y1)*(x3 – x2) – (y3 – y2)*(x2 – x1) < 0

So if the value of the above expression is smaller than 0, then the point p3 lies to the anti-clockwise of line (p1,p2).

 

Java Implementation 

Following Java function checks whether given 3 points are collinear, otherwise prints the orientation of the point p3 w.r.t the line (p1,p2).

 public static void checkCollinear(long x1, long y1, long x2, long y2, long x3, long y3) {
     long res = (y2 - y1) * (x3 - x2) - (y3 - y2) * (x2 - x1);

     if (res > 0) {
         System.out.println("Point 3 is clockwise to line (p1,p2)");
     } else if (res < 0) {
         System.out.println("Point 3 is anti-clockwise to line (p1,p2)");
     } else {
         System.out.println("Points are Collinear");
     }
 }

Invoking the above function:-

 public static void main(String[] args) {
     checkCollinear(1, 3, 4, 6, 7, 9);
     checkCollinear(1, 3, 4, 6, 8, 7);
     checkCollinear(1, 3, 4, 6, 5, 9);
 }

Output :-

Points are Collinear
Point 3 is clockwise to line (p1,p2)
Point 3 is anti-clockwise to line (p1,p2)

Problems which can be solved using this concept
1. Finding the Convex hull