Some Basic Linux Commands for beginners
pwd Print the present working directory with full path user1@raj:~/hadoop> pwd /home/user1/hadoop ls List contents of a Directory OR shows contents of the current directory if no directory is specified //List content of the directory /home ls /home //List content of the current directory ls //List contents of the Directory…
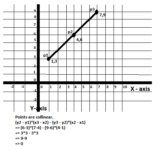
Checking Collinearity of 3 points and their orientation
Basics of ClassLoaders in Java
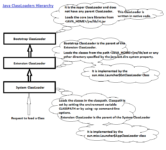
The Classloaders in Java dynamically load Java classes into the Java Virtual Machine. Usually classes are only loaded on demand. By default, Java uses three class loaders, when JVM starts. Bootstrap classloader Extension classloader System classloader Following figure shows the role of each ClassLoader:- The ClassLoaders in Java works on…
Java Basic Data Types
We will see the basic data types in Java. We will also write a simple program to assign values to different data types and print their values. Primitive data types byte byte is a 8 bit signed two’s complement integer. Can stores values from -128 to 127. byte bt =…
Writing a Simple Java Program
Here we will write a simple program in Java. Pre-requisites :- Java installed on your system. Download Java JDK and add JAVA_HOME environment variable to your system. Add ‘JAVA_HOME/bin’ path to your system’s PATH variable. IDE for Java- like eclipse. Assuming that you are done with the above requirements. Lets…
Creating and accessing Encrypted database in OrientDB using the graph APIs
OrientDB supports encrypting database content to prevent unauthorized users from accessing the data. The encryption support is available from version 2.2. To create/access an encrypted database, we need to provide a base64 encoded encryption key. OrientDB supports encryption at a database level and each database can be encrypted with different…
Depth First Search (DFS) for traversing a Graph
Using reflection to call methods of a Java class - A simple use case
We can use reflection feature of Java to invoke methods of a Java class. Suppose we have a class Employee, with getter methods for fields - name, age sex, salary, city. A user may want to send an array of property names to a method and based on the input…
Reading a File from same package in a Java Class
Sometimes we may need to read data from a file in a Java class and this file lies in the same package as that of the class. Different Java classes may need to read data from a file lying in their own package. If all the files in different packages…
Comparison of Storage formats in Hive - TEXTFILE vs ORC vs PARQUET
We will compare the different storage formats available in Hive. The comparison will be based on the size of the data on HDFS and time for executing a simple query. Cluster summary The performance is bench marked using a 5 node Hadoop cluster. Each node is a 8 core, 8…