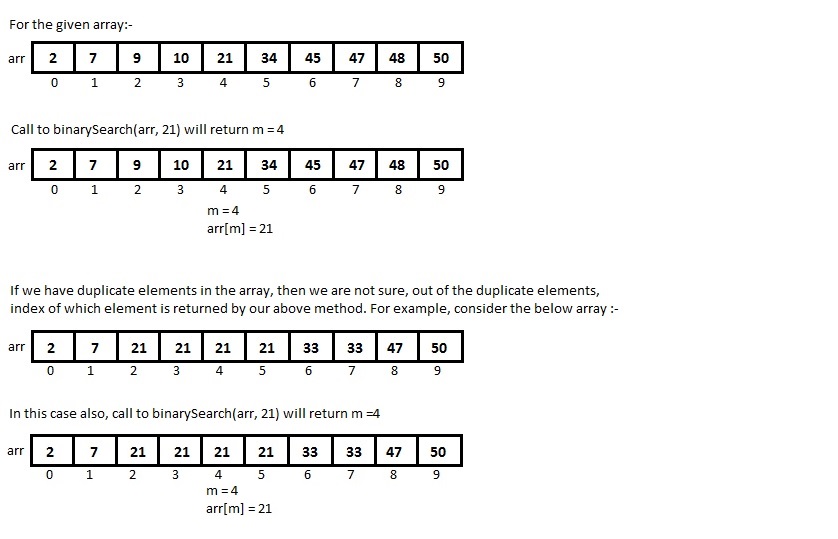
Binary Search is used to find an element in a sorted array. Complexity of binary search algorithm is log(N), where N is size of the sorted array. At each step of Binary Search we keep on dividing the array into half and try to find the required element in one of the half and ignore the remaining half.
Given :-
arr – the array from which we need to search
num – the element to be search in the array arr
Flavor 1:- Return index of the element if element is found in the array, else return -1
Here we will see the implementation of binary search which tries to find an element in the given sorted array. If the element is found it returns the index of the element else returns -1. Following code snippet shows implementation in Java:-
public int binarySearch(int[] arr, int num) {
int s = 0; // start index
int e = arr.length - 1; // end index
int m; // mid index
while (s <= e) {
m = (s + e) / 2;
if (arr[m] < num) {
s = m + 1; // num is on the right side of index m;
} else if (arr[m] > num) {
e = m - 1; // num is on the left side of index m;
} else {
return m; // num found at index m
}
}
return -1; // num is not found, return -1
}
What if we want to answer following questions using Binary search:-
- Get the index of first occurrence of any given element.
- Get the index of last occurrence of any given element.
- Get the index of largest element smaller than the given element.
- Get the index of smallest element greater than the given element.
- Find number of occurrences of a given element in the array.
We cannot use above binary search approach to get the answers for the above questions. We need to modify our approach a little bit and here comes other flavors of binary search.
Flavor 2:- Get the index of first occurrence of any given element. Return -1 if element not found.
In this approach we will see implementation of binary search which returns the index of first occurrence of any given element. Return -1 if the element is not found.
At the start we set s to to one less than zero, as in the while loop we are making sure that index s always contains element smaller than num. It may happen that the num is at the first index in the array.
We break the while loop when there are only 2 elements in our search window, one at index s and other at index e. In the while loop we make sure that the element at index s is always smaller than num and the element at index e is either equal to or greater than num. Therefore, at the end, outside the while loop, we need to check whether the element at index e is equal to num.
public int binarySearchFirstIndex(int[] arr, int num) {
int s = -1; // start index is set to one less than 0, as in the while loop
// below we are making sure that s index always contains element
// less than num. It may happen that the num is at the first index itself.
int e = arr.length - 1; // end index
int m; // mid index
while (e - s > 1) {
m = (s + e) / 2;
if (arr[m] < num) {
s = m; // num is on the right side of index m;
} else {
e = m; // num is on the left side of index m or at index m;
}
}
// At this point only 2 elements are present in our search window.
// The element at index s is smaller than num
// The element at index e is either equal to or greater than num,
// therefore we need to check whether the element at index e is equal to num.
if (arr[e] == num) {
return e;
} else {
return -1; // num is not found, return -1
}
}
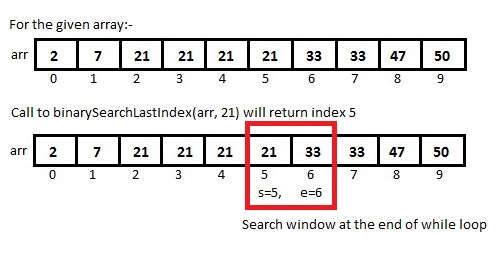
Flavor 3:- Get the index of last occurrence of any given element. Return -1 if element not found.
In this approach we will see implementation of binary search which returns the index of last occurrence of any given element. Return -1 if the element is not found.
At the start we set e to one more than last index in the array, as in the while loop we are making sure that index e always contains element greater than num. It may happen that the num is at the last index in the array.
We break the while loop when there are only 2 elements in our search window, one at index s and other at index e. In the while loop we make sure that the element at index e is always greater than num and the element at index s is either equal to or smaller than num. Therefore, at the end, outside the while loop, we need to check whether the element at index s is equal to num.
public int binarySearchLastIndex(int[] arr, int num) {
int s = 0; // start index
// set end index to one more than last index in the array, as in the while loop
// we are making sure that index e always contains element greater than num.
// It may happen that the num is at the last index in the array.
int e = arr.length;
int m; // mid index
while (e - s > 1) {
m = (s + e) / 2;
if (arr[m] <= num) {
s = m; // num is on the right side of index m or at index m;
} else {
e = m; // num is on the left side of index m;
}
}
// At this point only 2 elements are present in our search window.
// The element at index e is greater than num
// The element at index s is either equal to or smaller than num,
// therefore we need to check whether the element at index s is equal to num.
if (arr[s] == num) {
return s;
} else {
return -1; // num is not found, return -1
}
}
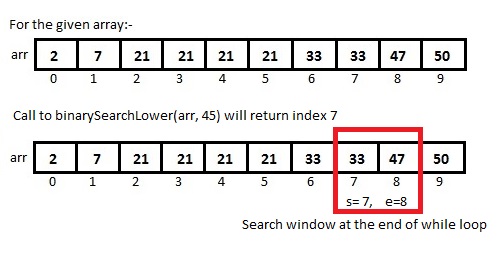
Flavor 4:- Get the index of largest element smaller than the given element.
In this approach we will see implementation of binary search which returns the index of largest element in the array which is smaller than the given element. This approach is similar to the approach of finding the first occurrence of any given element with slight modification.
At the start we set s to to one less than zero, as in the while loop we are making sure that index s always contains element smaller than num. It may happen that all elements in the array are greater than or equal to num, in this case -1 is returned.
We break the while loop when there are only 2 elements in our search window, one at index s and other at index e. In the while loop we make sure that the element at index s is always smaller than num and the element at index e is either equal to or greater than num. Return index s.
public int binarySearchLower(int[] arr, int num) {
// At the start we set s to to one less than zero, as in the while loop
// we are making sure that index s always contains element smaller than num.
// It may happen that all elements in the array are greater than or equal to num.
int s = -1;
int e = arr.length - 1; // end index
int m; // mid index
while (e - s > 1) {
m = (s + e) / 2;
if (arr[m] < num) {
s = m; // num is on the right side of index m;
} else {
e = m; // num is on the left side of index m or at index m;
}
}
// At this point only 2 elements are present in our search window.
// The element at index s is smaller than num
// The element at index e is either equal to or greater than num,
// therefore return s.
return s;
}
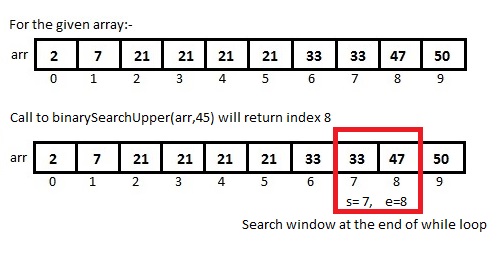
Flavor 5:- Get the index of smallest element greater than the given element
In this approach we will see implementation of binary search which returns the index of smallest element in the given array which is greater than the given element. This approach is similar to the approach of finding the last occurrence of any given element with slight modification.
At the start we set e to one more than last index in the array, as in the while loop we are making sure that index e always contains element greater than num. It may happen that all elements in the array are smaller than or equal to num, in this case -1 is returned.
We break the while loop when there are only 2 elements in our search window, one at index s and other at index e. In the while loop we make sure that the element at index e is always greater than num and the element at index s is either equal to or smaller than num. Return index e.
public int binarySearchUpper(int[] arr, int num) {
int s = 0; // start index
// set end index to one more than last index in the array, as in the while loop
// we are making sure that index e always contains element greater than num.
// It may happen that all elements in the array are smaller than or equal to num.
int e = arr.length;
int m; // mid index
while (e - s > 1) {
m = (s + e) / 2;
if (arr[m] <= num) {
s = m; // num is on the right side of index m or at index m;
} else {
e = m; // num is on the left side of index m;
}
}
// At this point only 2 elements are present in our search window.
// The element at index e is greater than num
// The element at index s is either equal to or smaller than num
if (e < arr.length) {
return e;
} else {
return -1;
}
}
Some problems which can be solved by using different flavors of Binary Search:-
1. Find number of occurrences of a given element in the array.
Solution:- This can be simply found by –
binarySearchLastIndex(arr, num) – binarySearchFirstIndex(arr, num) + 1
2. Find number of elements int the array strictly smaller than the given element.
Solution:- This can be found by –
binarySearchLower(arr, num) + 1
3. Find number of elements int the array smaller than or equal to the given element.
Solution:- This can be found by –
binarySearchUpper(arr, num)
4. Find number of elements int the array strictly greater than the given element.
Solution:- This can be found by –
arr.length – binarySearchUpper(arr, num)
4. Find number of elements int the array greater than or equal to the given element.
Solution:- This can be found by –
arr.length – binarySearchLower(arr, num) -1
Practice Problems:-